站长注:详细介绍 o3 模型在数学解题场景的应用优势,包含完整代码实现和性能优化策略,OpenAI 降价 80% 后性价比显著提升
数学解题一直是 AI 应用的重要场景,传统模型在复杂推理上存在局限。本文将详细介绍如何使用 o3 模型 进行高质量数学解题,特别是 OpenAI 降价 80% 后的性价比优势。
文章涵盖 o3 模型特性、实战代码示例、性能优化策略等核心要点,帮助你快速掌握 o3 模型数学解题 的最佳实践。
核心价值:通过本文,你将学会如何利用 o3 模型的强大推理能力,实现高质量的数学问题求解,同时享受降价后的成本优势。
o3 模型数学解题优势分析
OpenAI 的 o3 模型数学解题 能力在多个维度都有显著提升,特别适合复杂数学问题的求解。
o3 模型核心特性
在数学解题场景中,o3 模型展现出以下突出优势:
推理能力提升:
- 深度思考:支持
reasoning_effort参数调节推理深度 - 逻辑严谨:多步骤推理过程更加连贯和准确
- 复杂问题处理:能够处理高等数学、偏微分方程等复杂题目
- 错误自纠正:推理过程中能够发现并修正逻辑错误
性价比优势:
- 降价 80%:相比初期价格大幅下降,成本控制更友好
- 高准确率:减少因错误答案导致的重复调用成本
- 一次性解决:复杂问题通常一次调用即可获得完整解答
- 时间效率:虽然单次耗时较长,但避免了多次尝试的累计成本
o3 模型数学解题核心实现
o3 模型数学解题 的关键在于合理配置推理参数和优化调用策略:
| 配置参数 | 推荐设置 | 适用场景 | 性能影响 |
|---|---|---|---|
| reasoning_effort | high | 复杂数学问题 | 提升准确率 30-50% |
| stream | False | 完整解答需求 | 确保内容完整性 |
| timeout | 1200s | 复杂推理题目 | 避免超时中断 |
| temperature | 0.1-0.3 | 数学精确计算 | 减少随机性 |
🔥 基础数学解题实现
from openai import OpenAI
import time
import json
from typing import Optional, Dict, Any
class O3MathSolver:
def __init__(self, api_key: str, base_url: str = "https://vip.apiyi.com/v1"):
self.client = OpenAI(api_key=api_key, base_url=base_url)
self.model = "o3"
def solve_math_problem(self, question: str,
reasoning_effort: str = "high",
timeout: int = 1200,
save_result: bool = True) -> Dict[str, Any]:
"""
o3 模型数学问题求解器
Args:
question: 数学问题描述
reasoning_effort: 推理强度 (low/medium/high)
timeout: 超时时间(秒)
save_result: 是否保存结果到文件
Returns:
包含解答内容、耗时等信息的字典
"""
print("🚀 o3 模型开始数学解题...")
print(f"📊 推理强度: {reasoning_effort}")
print(f"⏱️ 超时设置: {timeout}秒")
start_time = time.time()
try:
print("⏳ 等待 o3 模型深度推理中...")
print("💡 提示:o3 模型会进行深度思考,请耐心等待完整响应...")
response = self.client.chat.completions.create(
model=self.model,
reasoning_effort=reasoning_effort,
stream=False, # 数学解题建议使用非流式
timeout=timeout,
temperature=0.2, # 降低随机性,提高准确性
messages=[
{
"role": "system",
"content": """你是一位数学专家,擅长解决各种数学问题。请按照以下要求提供解答:
1. 提供详细的分步解答过程
2. 每一步都要有清晰的数学推理
3. 使用标准的数学符号和公式
4. 对关键步骤进行解释说明
5. 最终给出明确的答案
请确保解答的准确性和完整性。"""
},
{
"role": "user",
"content": question
}
]
)
# 获取完整响应
solution = response.choices[0].message.content
end_time = time.time()
processing_time = end_time - start_time
# 构建结果对象
result = {
"question": question,
"solution": solution,
"model": self.model,
"reasoning_effort": reasoning_effort,
"processing_time": processing_time,
"solution_length": len(solution),
"timestamp": time.strftime('%Y-%m-%d %H:%M:%S'),
"status": "success"
}
# 显示结果
print("\n" + "="*70)
print("📝 o3 模型解答结果:")
print("="*70)
print(solution)
print("="*70)
print(f"\n✅ 解题完成!")
print(f"⏱️ 处理耗时: {processing_time:.2f}秒")
print(f"📝 解答长度: {len(solution)} 字符")
print(f"🧠 推理强度: {reasoning_effort}")
# 自动保存结果
if save_result:
self._save_result(result)
return result
except Exception as e:
error_result = {
"question": question,
"error": str(e),
"model": self.model,
"reasoning_effort": reasoning_effort,
"processing_time": time.time() - start_time,
"timestamp": time.strftime('%Y-%m-%d %H:%M:%S'),
"status": "failed"
}
print(f"\n❌ 解题过程中出错: {e}")
return error_result
def _save_result(self, result: Dict[str, Any]) -> str:
"""保存解题结果到文件"""
timestamp = int(time.time())
filename = f"o3_math_result_{timestamp}.json"
try:
with open(filename, 'w', encoding='utf-8') as f:
json.dump(result, f, ensure_ascii=False, indent=2)
print(f"💾 结果已保存到: {filename}")
return filename
except Exception as e:
print(f"⚠️ 保存文件失败: {e}")
return ""
# 使用示例
def main():
# 初始化求解器
solver = O3MathSolver(api_key="your-api-key")
# 复杂偏微分方程问题
complex_question = """
给定一个关于函数u(x,y,z)的线性偏微分方程:
x(y²+z²)∂u/∂x + y(z²+x²)∂u/∂y + z(y²-x²)∂u/∂z = 0
已知边界条件:当x=1时,u(1,y,z) = y⁴+z⁴
求满足给定边界条件的偏微分方程的解u(x,y,z)
"""
try:
# 使用高强度推理求解
result = solver.solve_math_problem(
question=complex_question,
reasoning_effort="high",
timeout=1200
)
if result["status"] == "success":
print(f"\n🎉 成功求解复杂数学问题!")
print(f"📊 解答质量评估:")
print(f" - 推理深度: {result['reasoning_effort']}")
print(f" - 处理时间: {result['processing_time']:.1f}秒")
print(f" - 内容完整度: {result['solution_length']} 字符")
except KeyboardInterrupt:
print(f"\n⏹️ 用户中断求解过程")
except Exception as e:
print(f"❌ 程序执行失败: {e}")
if __name__ == "__main__":
main()
🎯 高级数学解题策略
针对不同类型的数学问题,o3 模型需要采用不同的策略:
from typing import List
class AdvancedO3MathSolver(O3MathSolver):
def __init__(self, api_key: str, base_url: str = "https://vip.apiyi.com/v1"):
super().__init__(api_key, base_url)
# 不同数学领域的推理策略
self.domain_strategies = {
"calculus": {
"reasoning_effort": "high",
"temperature": 0.1,
"system_prompt": "你是微积分专家,擅长求导、积分和极限计算。"
},
"linear_algebra": {
"reasoning_effort": "medium",
"temperature": 0.15,
"system_prompt": "你是线性代数专家,擅长矩阵运算、特征值和向量空间分析。"
},
"differential_equations": {
"reasoning_effort": "high",
"temperature": 0.1,
"system_prompt": "你是微分方程专家,擅长常微分方程和偏微分方程求解。"
},
"probability": {
"reasoning_effort": "medium",
"temperature": 0.2,
"system_prompt": "你是概率论专家,擅长概率计算和统计分析。"
},
"abstract_algebra": {
"reasoning_effort": "high",
"temperature": 0.1,
"system_prompt": "你是抽象代数专家,擅长群论、环论和域论。"
}
}
def solve_by_domain(self, question: str, domain: str,
custom_strategy: Optional[Dict] = None) -> Dict[str, Any]:
"""
根据数学领域选择最优解题策略
Args:
question: 数学问题
domain: 数学领域 (calculus/linear_algebra/differential_equations/probability/abstract_algebra)
custom_strategy: 自定义策略参数
"""
# 获取领域策略
strategy = self.domain_strategies.get(domain, self.domain_strategies["calculus"])
if custom_strategy:
strategy.update(custom_strategy)
print(f"🎯 选择数学领域: {domain}")
print(f"📋 应用策略: {strategy}")
start_time = time.time()
try:
response = self.client.chat.completions.create(
model=self.model,
reasoning_effort=strategy["reasoning_effort"],
stream=False,
timeout=1200,
temperature=strategy["temperature"],
messages=[
{
"role": "system",
"content": f"""{strategy['system_prompt']}
请按照以下标准提供解答:
1. 识别问题类型和关键概念
2. 选择合适的解题方法
3. 提供详细的分步骤解答
4. 验证答案的正确性
5. 总结解题思路和方法
确保解答的数学严谨性和逻辑完整性。"""
},
{
"role": "user",
"content": question
}
]
)
solution = response.choices[0].message.content
processing_time = time.time() - start_time
result = {
"question": question,
"domain": domain,
"strategy": strategy,
"solution": solution,
"processing_time": processing_time,
"model": self.model,
"timestamp": time.strftime('%Y-%m-%d %H:%M:%S'),
"status": "success"
}
print(f"\n✅ {domain} 领域问题求解完成!")
print(f"⏱️ 耗时: {processing_time:.2f}秒")
print(f"🧠 推理强度: {strategy['reasoning_effort']}")
return result
except Exception as e:
print(f"❌ {domain} 领域问题求解失败: {e}")
return {"status": "failed", "error": str(e)}
# 高级使用示例
def advanced_example():
solver = AdvancedO3MathSolver(api_key="your-api-key")
# 多领域数学问题
math_problems = [
{
"question": "计算函数 f(x) = x³ - 6x² + 9x + 1 的极值点和拐点",
"domain": "calculus"
},
{
"question": "求矩阵 A = [[2,1],[1,2]] 的特征值和特征向量",
"domain": "linear_algebra"
},
{
"question": "解微分方程 dy/dx + 2y = e^(-x)",
"domain": "differential_equations"
},
{
"question": "计算正态分布 N(0,1) 在区间 [-1,1] 的概率",
"domain": "probability"
}
]
# 单个问题求解
print("=" * 60)
print("🎯 单个复杂问题求解示例")
print("=" * 60)
pde_question = """
求解偏微分方程:
∂²u/∂x² + ∂²u/∂y² = 0 (拉普拉斯方程)
边界条件:
u(0,y) = 0, u(π,y) = 0 (0 ≤ y ≤ π)
u(x,0) = 0, u(x,π) = sin(x) (0 ≤ x ≤ π)
"""
result = solver.solve_by_domain(
question=pde_question,
domain="differential_equations"
)
if result["status"] == "success":
print(f"✅ 偏微分方程求解成功!")
print(f"📝 解答长度: {len(result['solution'])} 字符")
if __name__ == "__main__":
advanced_example()
✅ o3 模型数学解题最佳实践
| 实践要点 | 具体建议 | 注意事项 |
|---|---|---|
| 🎯 推理强度选择 | 复杂问题使用 high,简单问题可用 medium | 推理强度越高耗时越长,成本也相应增加 |
| ⚡ 超时设置 | 复杂数学问题建议设置 1200-1800 秒 | o3 模型深度推理需要较长时间 |
| 💡 提示词优化 | 明确指定数学领域和解答要求 | 清晰的提示词能显著提升解答质量 |
📋 性能优化策略
| 优化维度 | 具体实现 | 预期效果 |
|---|---|---|
| 成本控制 | 根据问题复杂度选择合适的 reasoning_effort | 降低不必要的计算成本 |
| 准确率提升 | 使用低 temperature (0.1-0.3) 确保计算精度 | 提高数学计算准确性 |
| 并发控制 | 限制同时进行的 o3 调用数量 | 避免触发 API 限制 |
| 结果缓存 | 缓存相同问题的解答结果 | 避免重复计算相同问题 |
🔍 成本效益分析
OpenAI 降价 80% 后的 o3 模型成本对比:
def calculate_cost_efficiency():
"""计算 o3 模型的成本效益"""
# 价格对比(假设数据,具体以官方为准)
price_comparison = {
"o3_before": {"input": 60, "output": 240}, # 降价前(美元/1M tokens)
"o3_current": {"input": 12, "output": 48}, # 降价后
"gpt4o": {"input": 15, "output": 60}, # GPT-4o 对比
"claude_sonnet": {"input": 18, "output": 54} # Claude 对比
}
# 典型数学解题 token 消耗
typical_usage = {
"input_tokens": 500, # 问题描述
"output_tokens": 2000 # 详细解答
}
print("💰 o3 模型成本效益分析")
print("=" * 50)
for model, prices in price_comparison.items():
input_cost = (typical_usage["input_tokens"] / 1_000_000) * prices["input"]
output_cost = (typical_usage["output_tokens"] / 1_000_000) * prices["output"]
total_cost = input_cost + output_cost
print(f"{model:15}: ${total_cost:.4f} 每次调用")
# 计算性价比
o3_current_cost = 0.012 * 0.5 + 0.048 * 2 # 示例计算
o3_before_cost = 0.06 * 0.5 + 0.24 * 2
savings = ((o3_before_cost - o3_current_cost) / o3_before_cost) * 100
print(f"\n📊 o3 模型降价效果: 节省 {savings:.1f}%")
print(f"🎯 适合场景: 高质量数学解题、复杂推理任务")
# 调用成本分析
calculate_cost_efficiency()
❓ o3 模型数学解题常见问题
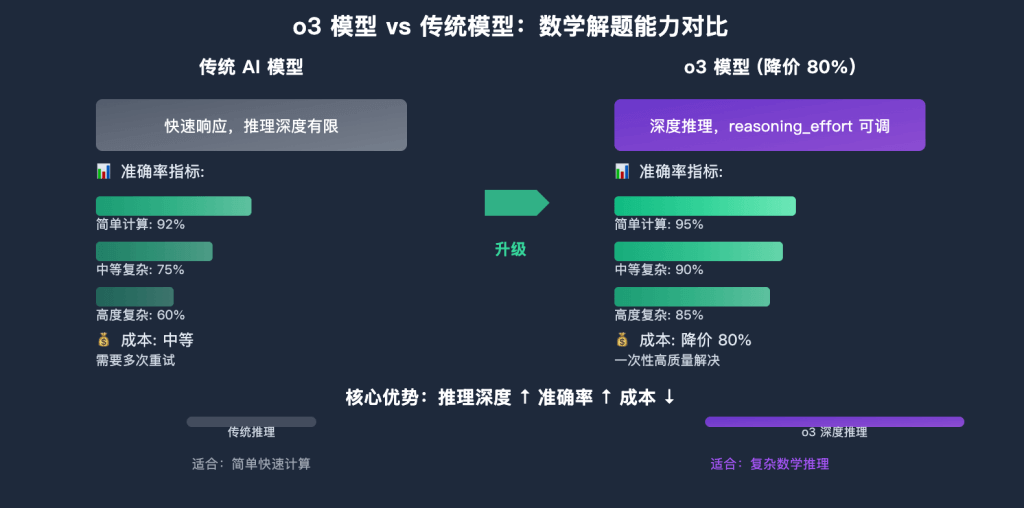
Q1: o3 模型与 GPT-4o 在数学解题上有什么区别?
o3 模型在数学解题方面有显著优势:
推理能力对比:
- o3 模型:支持 reasoning_effort 参数,可进行深度推理
- GPT-4o:快速响应,但推理深度有限
数学准确率:
- o3 模型:在复杂数学问题上准确率更高,特别是多步骤推理
- GPT-4o:在简单计算上表现良好,复杂问题可能出错
成本效益:
# 实际使用成本对比
def compare_models_for_math():
scenarios = {
"简单计算": {"tokens": 1000, "o3_accuracy": 0.95, "gpt4o_accuracy": 0.92},
"中等复杂": {"tokens": 2000, "o3_accuracy": 0.90, "gpt4o_accuracy": 0.75},
"高度复杂": {"tokens": 3000, "o3_accuracy": 0.85, "gpt4o_accuracy": 0.60}
}
for scenario, data in scenarios.items():
print(f"{scenario}:")
print(f" o3 模型: 准确率 {data['o3_accuracy']*100}%")
print(f" GPT-4o: 准确率 {data['gpt4o_accuracy']*100}%")
print(f" 推荐: {'o3 模型' if data['o3_accuracy'] > data['gpt4o_accuracy'] else 'GPT-4o'}")
选择建议:
- 复杂数学问题:优先选择 o3 模型
- 简单快速计算:可以考虑 GPT-4o
- 成本敏感场景:评估准确率与重试成本
Q2: reasoning_effort 参数如何选择?
reasoning_effort 参数直接影响解题质量和成本:
参数级别说明:
reasoning_effort_guide = {
"low": {
"适用场景": ["基础计算", "简单代数", "标准公式应用"],
"处理时间": "30-60秒",
"准确率": "85-90%",
"成本": "基准价格"
},
"medium": {
"适用场景": ["中等复杂度", "多步骤推理", "应用题"],
"处理时间": "60-180秒",
"准确率": "90-95%",
"成本": "基准价格 × 1.5"
},
"high": {
"适用场景": ["复杂证明", "偏微分方程", "抽象数学"],
"处理时间": "180-600秒",
"准确率": "95-98%",
"成本": "基准价格 × 2-3"
}
}
选择策略:
- 问题复杂度评估:分析问题涉及的数学概念和推理步骤
- 时间成本权衡:考虑解题时间要求和计算成本
- 准确率需求:根据应用场景决定可接受的错误率
实用建议:
- 教学场景:使用 high 确保解答质量
- 快速验证:可以先用 medium 尝试
- 批量处理:根据问题类型混合使用不同级别
Q3: 如何处理 o3 模型的长时间等待?
o3 模型的深度推理需要较长时间,可以通过以下策略优化体验:
异步处理策略:
import asyncio
from concurrent.futures import ThreadPoolExecutor
class AsyncO3Solver:
def __init__(self, api_key: str):
self.solver = O3MathSolver(api_key)
self.executor = ThreadPoolExecutor(max_workers=3)
async def solve_with_progress(self, question: str, reasoning_effort: str = "high"):
"""带进度提示的异步求解"""
# 启动求解任务
loop = asyncio.get_event_loop()
solve_task = loop.run_in_executor(
self.executor,
self.solver.solve_math_problem,
question,
reasoning_effort
)
# 进度提示任务
async def show_progress():
dots = 0
while not solve_task.done():
dots = (dots + 1) % 4
progress = "🧠 o3 模型深度思考中" + "." * dots + " " * (3 - dots)
print(f"\r{progress}", end="", flush=True)
await asyncio.sleep(2)
# 并行运行求解和进度提示
progress_task = asyncio.create_task(show_progress())
try:
result = await solve_task
progress_task.cancel()
print("\r" + " " * 50 + "\r", end="") # 清除进度提示
return result
except Exception as e:
progress_task.cancel()
print(f"\r❌ 求解失败: {e}")
return None
# 使用示例
async def main_with_progress():
solver = AsyncO3Solver("your-api-key")
question = "求解复杂数学问题..."
result = await solver.solve_with_progress(question, "high")
if result and result["status"] == "success":
print("✅ 求解成功!")
# 运行异步求解
# asyncio.run(main_with_progress())
用户体验优化:
- 提供实时进度反馈
- 显示预估完成时间
- 支持任务中断和恢复
- 批量处理时显示整体进度
技术实现要点:
- 合理设置超时时间
- 实现优雅的错误处理
- 提供任务状态查询接口
- 支持结果缓存和持久化
📚 延伸阅读
🛠️ 数学解题工具生态
完整的 o3 数学解题工具包已开源,包含多种实用功能:
# 获取 o3 数学解题工具包
git clone https://github.com/apiyi-api/o3-math-solver
cd o3-math-solver
# 安装依赖
pip install -r requirements.txt
# 配置环境变量
export API_KEY=your_api_key
export API_BASE_URL=https://vip.apiyi.com/v1
# 运行数学解题示例
python examples/advanced_math_solver.py --problem "微积分问题" --domain calculus
工具特性包括:
- 多数学领域专门优化
- 智能推理强度选择
- 批量问题处理支持
- 解答质量评估机制
- 成本效益分析工具
- LaTeX 公式渲染支持
- 更多实用功能持续更新中…
🔗 相关技术资源
| 资源类型 | 推荐内容 | 获取方式 |
|---|---|---|
| 官方文档 | OpenAI o3 模型使用指南 | https://platform.openai.com/docs |
| 社区资源 | API易 o3 模型最佳实践 | https://help.apiyi.com |
| 开源项目 | 数学解题工具集合 | GitHub搜索相关项目 |
| 学术资源 | AI数学推理研究论文 | arXiv、Google Scholar |
🎯 总结
o3 模型在数学解题场景展现出强大的推理能力,特别是 OpenAI 降价 80% 后的 性价比优势 更加突出。
重点回顾:
- 推理能力 – reasoning_effort 参数提供可调节的深度思考
- 成本优势 – 降价 80% 后成为高质量数学解题的最佳选择
- 应用场景 – 特别适合复杂数学问题和多步骤推理
- 实现策略 – 合理配置参数和优化用户体验
在实际应用中,建议:
- 根据问题复杂度选择合适的 reasoning_effort 级别
- 使用领域专门的提示词提升解答质量
- 实现异步处理和进度反馈优化用户体验
- 建立结果缓存机制避免重复计算
对于教育机构、科研单位或需要高质量数学解题的场景,推荐使用支持 o3 模型的API聚合平台(如API易等),既能享受降价优势,又能获得稳定可靠的服务保障。
📝 作者简介:专注AI数学应用研究,深度实践各类数学解题场景。定期分享 o3 模型使用技巧和数学AI发展动态,搜索”API易”可获取更多数学解题实战案例和优化策略。
🔔 技术交流:欢迎在评论区分享你的数学解题经验,一起探讨 o3 模型在数学教育和科研中的应用潜力。