站长注：深度解析 DeepSeek-Prover-V2 模型的核心特性、技术原理及在 Lean 4 形式化定理证明中的应用，API易平台现已全面支持

DeepSeek-Prover-V2 是一款专为形式化数学定理证明设计的大型语言模型，特别针对 Lean 4 环境优化。本文将详细介绍这一突破性模型的技术原理、性能表现及使用方法，帮助数学研究者、形式化验证专家和相关开发者充分释放其潜力。

欢迎免费试用 API易，3 分钟跑通 API 调用 www.apiyi.com
支持 DeepSeek 全系列模型（包括最新的 Prover-V2），让形式化定理证明更简单
注册可送 1.1 美金额度起，约 300万 Tokens 额度体验。立即免费注册
加站长个人微信：8765058，发送你《大模型使用指南》等资料包，并加赠 1 美金额度。

DeepSeek-Prover-V2 API 背景介绍

DeepSeek-Prover-V2 是 DeepSeek AI 团队最新发布的开源形式化定理证明大模型，专为 Lean 4 交互式证明助手环境设计。与传统的数学语言模型不同，DeepSeek-Prover-V2 能够将非形式化的数学推理转化为严格的形式化证明，大幅提升了复杂数学问题的证明能力和效率。

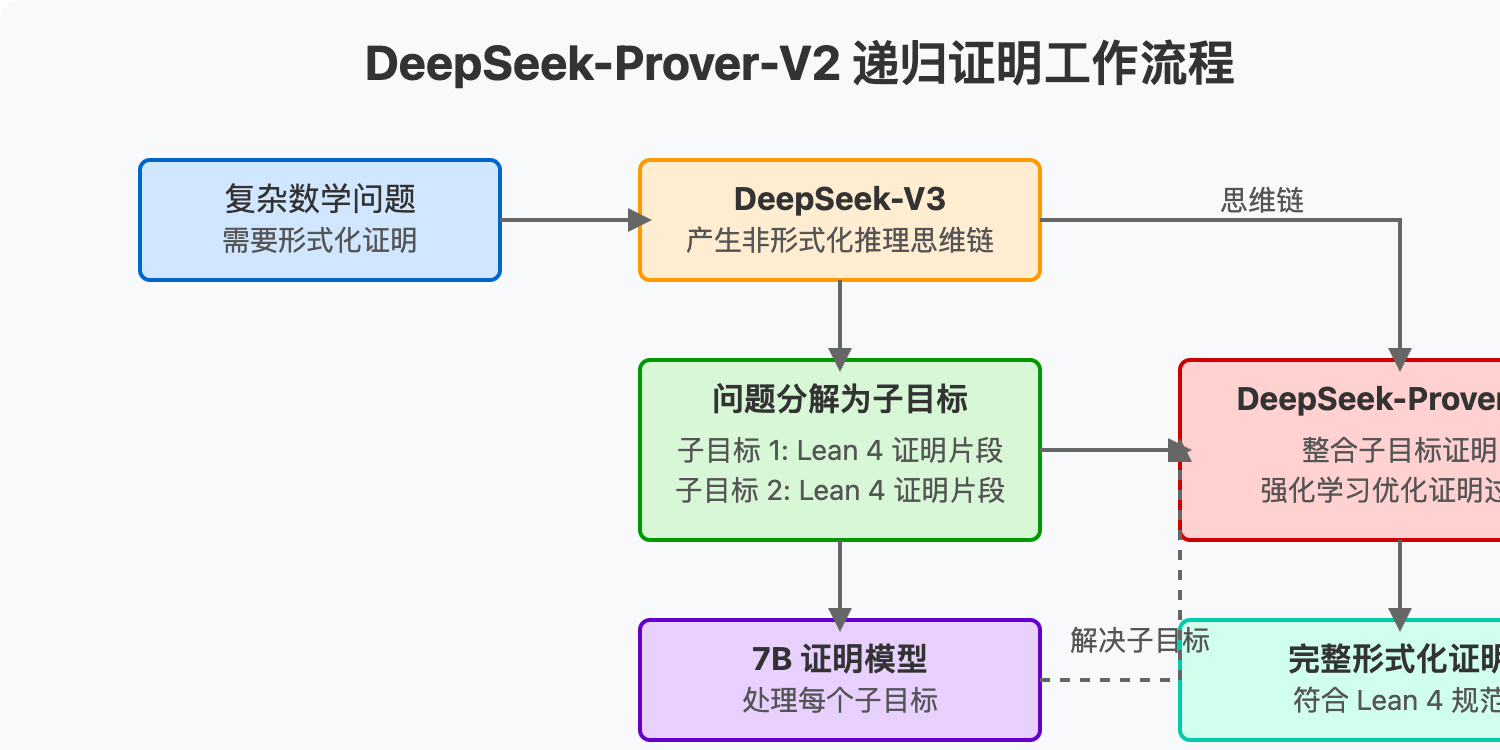
该模型通过递归定理证明流程收集初始化数据，由 DeepSeek-V3 提供强大支持。其冷启动训练过程首先通过提示 DeepSeek-V3 将复杂问题分解为一系列子目标，然后将已解决子目标的证明综合为思维链过程，结合 DeepSeek-V3 的逐步推理，为强化学习创建初始冷启动。这一过程使模型能够将非形式化和形式化数学推理集成到统一的框架中。

DeepSeek-Prover-V2-671B 模型在神经网络定理证明领域达到了最先进水平，在 MiniF2F 测试集上达到了 88.9% 的通过率，并解决了 PutnamBench 中 658 个问题中的 49 个，展现了其在处理高难度数学证明方面的卓越能力。

deepseek-prover-v2-api-guide 图示

DeepSeek-Prover-V2 API 核心功能

递归证明搜索与冷启动数据合成

DeepSeek-Prover-V2 通过创新的递归定理证明流程构建冷启动数据集。该流程利用 DeepSeek-V3 作为子目标分解和形式化的统一工具。具体而言，模型会提示 DeepSeek-V3 将定理分解为高级证明草图，同时将这些证明步骤形式化为 Lean 4 代码，从而生成一系列子目标。

为减轻计算负担，团队使用较小的 7B 模型处理每个子目标的证明搜索。当复杂问题的所有分解步骤都得到解决后，将完整的逐步形式化证明与 DeepSeek-V3 的思维链配对，创建冷启动推理数据。

这种方法特别适合那些 7B 证明模型无法端到端解决，但所有分解子目标已成功解决的挑战性问题。通过组合所有子目标的证明，构建出原始问题的完整形式化证明，再附加 DeepSeek-V3 的思维链（概述相应的引理分解），产生非形式化推理和随后形式化的连贯综合。

基于合成冷启动数据的强化学习

在合成冷启动数据上微调证明模型后，DeepSeek 团队进行了强化学习阶段，进一步增强模型将非形式化推理与形式化证明构建相结合的能力。遵循推理模型的标准训练目标，他们使用二元正确-错误反馈作为主要奖励监督形式。

强化学习使模型能够从自己的错误中学习，逐步提高其生成有效形式化证明的能力。这一训练过程特别注重模型在复杂数学推理中的鲁棒性和准确性，使其能够处理各种难度和类型的数学问题。

ProverBench：AIME 和教科书问题的形式化

DeepSeek 团队还引入了 ProverBench，这是一个包含 325 个问题的基准数据集。其中 15 个是从最近的 AIME 竞赛（AIME 24 和 25）中的数论和代数问题形式化而来，提供真实的高中竞赛级别挑战。其余 310 个问题来自精选的教科书示例和教育教程，贡献了多样化且具有教学基础的形式化数学问题集合。

ProverBench 涵盖了广泛的数学领域，包括：

  • 数论（40个问题）
  • 初等代数（30个问题）
  • 线性代数（50个问题）
  • 抽象代数（40个问题）
  • 微积分（90个问题）
  • 实分析（30个问题）
  • 复分析（10个问题）
  • 泛函分析（10个问题）
  • 概率论（10个问题）

这个基准旨在实现更全面的评估，涵盖高中竞赛问题和本科水平的数学。通过在这些不同领域的问题上测试模型，可以更全面地了解 DeepSeek-Prover-V2 的能力和局限性。

API 易，新用户赠送 1美金欢迎试用体验

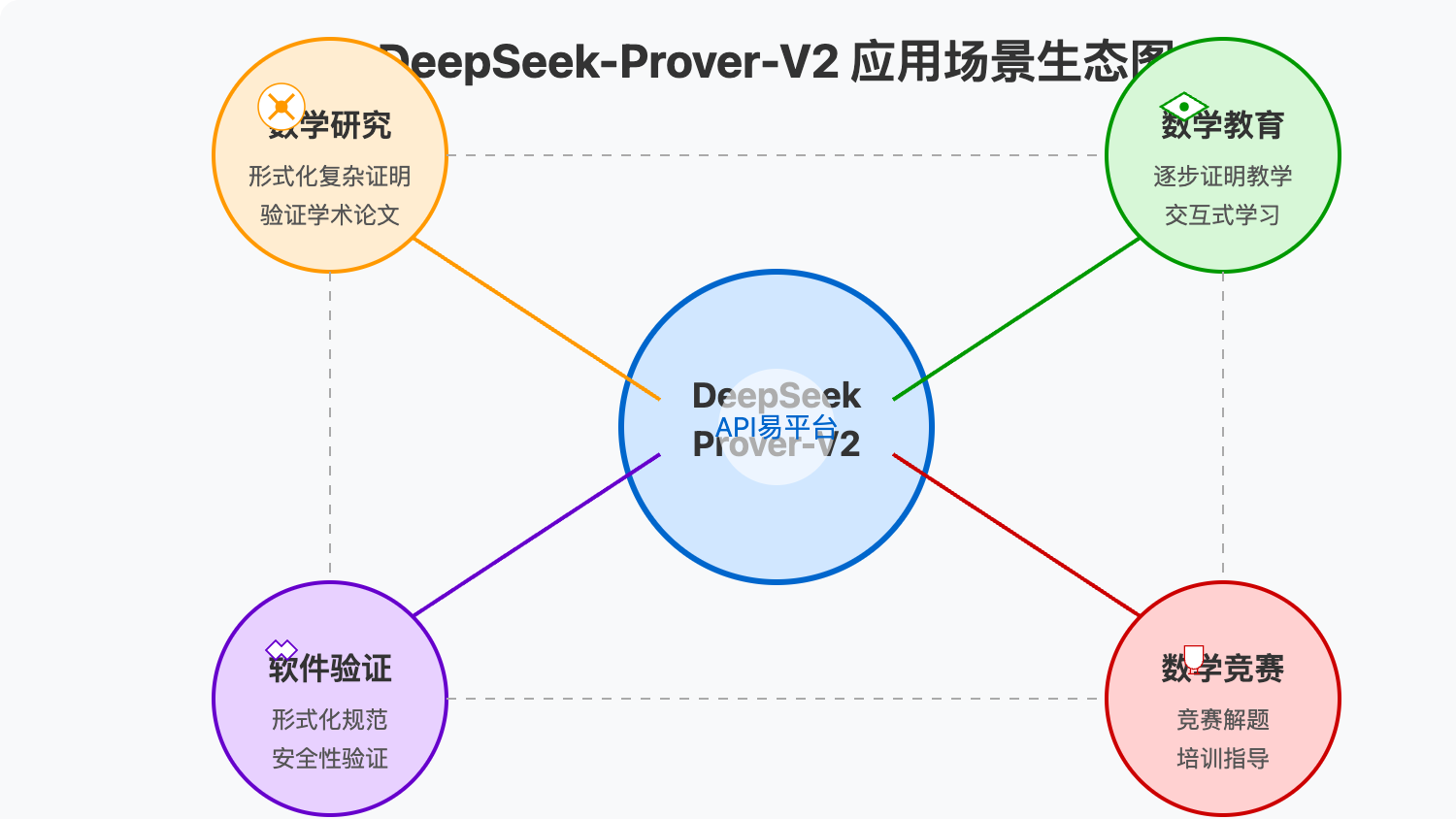
DeepSeek-Prover-V2 API 应用场景

DeepSeek-Prover-V2 的强大能力使其在多个领域具有广泛的应用潜力：

数学研究与证明验证

研究数学家可以利用 DeepSeek-Prover-V2 来探索新的定理证明思路，或验证现有证明的正确性。这对于复杂定理的证明尤其有价值，可以大幅减少人工验证的时间和错误率。

具体应用包括：

  • 协助数学研究人员形式化复杂证明
  • 验证学术论文中的数学证明
  • 发现现有证明中的潜在错误或缺陷
  • 探索多种证明路径和方法

形式化数学教育

DeepSeek-Prover-V2 可以成为强大的教育工具，帮助学生理解形式化证明的构建过程和严格推理的重要性：

  • 生成详细的、逐步的证明过程，帮助学生学习
  • 为不同难度的数学问题提供证明思路
  • 将非形式化的直觉转化为严格的形式化证明，展示数学思维过程
  • 支持交互式学习环境，让学生能够尝试不同的证明方法

软件验证与形式化方法

在软件工程领域，DeepSeek-Prover-V2 可以辅助开发人员进行程序正确性的形式化验证：

  • 协助编写关键系统组件的形式化规范
  • 验证算法的正确性和安全性
  • 在密码学协议设计中应用形式化证明
  • 支持航空航天、医疗、金融等高安全性要求领域的软件验证

数学竞赛培训与解题

DeepSeek-Prover-V2 特别适合数学竞赛培训，尤其是针对 AIME、IMO 等高水平数学竞赛：

  • 生成详细的竞赛题目解题思路和证明
  • 分析复杂问题，提供多种解题策略
  • 帮助教练开发训练材料和挑战性问题
  • 为学生提供个性化的解题指导

deepseek-prover-v2-api-guide 图示

DeepSeek-Prover-V2 API 开发指南

1. 模型选择

模型服务介绍

本站均为官方源头转发，价格略有优势，聚合各种优秀大模型，使用起来很方便。
企业级专业稳定的OpenAI o1/Deepseek R1/Gemini 等全模型官方同源接口的中转分发。不限速，不过期，不惧封号，按量计费，长期可靠服务；让技术助力科研、公益事业！

当前模型推荐（均为稳定供给）

全部模型和价格请看网站后台 https://www.apiyi.com/account/pricing

  1. DeepSeek 系列

    • deepseek-prover-v2：本文重点介绍的形式化定理证明专用模型（推荐指数：⭐⭐⭐⭐⭐）
    • deepseek-v3：多功能通用大模型，支持数学推理
    • deepseek-r1：推理增强型模型，适合复杂逻辑问题

  2. 其他数学增强型模型

    • claude-3-7-sonnet-20250219：强大的数学能力，但形式化证明不如专用模型
    • gpt-4o：综合表现优异，具备数学推理能力，但专业性不如 deepseek-prover-v2

场景推荐

  1. 形式化数学证明场景

    • 首选：deepseek-prover-v2（专为 Lean 4 环境设计）
    • 特点：最高的定理证明通过率，专业数学表达，形式化支持

  2. 数学教育和学习场景

    • 首选：deepseek-prover-v2 + deepseek-v3（配合使用）
    • 特点：前者提供形式化证明，后者提供直观解释

  3. 软件验证与形式化方法场景

    • 首选：deepseek-prover-v2
    • 特点：准确的逻辑推理，适合严格的形式化要求

注意：具体价格请参考 API易价格页面，DeepSeek-Prover-V2 按 Input: $0.5 / M Tokens，Output: $2 / M Tokens 收费。

实践示例

以下是使用 DeepSeek-Prover-V2 API 解决数学证明问题的完整示例：

import os
from openai import OpenAI

# 初始化客户端
client = OpenAI(
    api_key="YOUR_APIYI_KEY",  # 替换为您的 API易 API 密钥
    base_url="https://vip.apiyi.com/v1"  # API易的基础URL
)

# 定理证明示例：证明平方根2是无理数
def prove_sqrt2_irrational():
    prompt = """
    请使用 Lean 4 形式化证明以下定理：平方根2是无理数。
    
    具体来说，证明不存在整数 p 和 q (q ≠ 0) 使得 p/q = √2。
    
    请给出完整的形式化证明过程，包括所有必要的引理和定义。
    """
    
    print("正在使用 DeepSeek-Prover-V2 生成证明...")
    
    response = client.chat.completions.create(
        model="deepseek-prover-v2",
        messages=[
            {"role": "system", "content": "You are a formal mathematics assistant specialized in Lean 4 theorem proving."},
            {"role": "user", "content": prompt}
        ],
        temperature=0.2,  # 较低的温度使输出更加确定性
        max_tokens=2048   # 根据需要调整
    )
    
    proof = response.choices[0].message.content
    return proof

# 定义一个函数处理更复杂的数学问题
def solve_math_problem(problem_description):
    # 构建系统提示词，引导模型生成高质量的形式化证明
    system_prompt = """
    You are a formal mathematics assistant specialized in Lean 4 theorem proving.
    
    Follow these steps:
    1. Analyze the mathematical problem carefully
    2. Identify the key concepts and theorems needed
    3. Plan a proof strategy using informal reasoning
    4. Translate this reasoning into formal Lean 4 code
    5. Provide a complete, step-by-step formal proof
    6. Add explanatory comments to clarify the reasoning
    
    Your goal is to produce a correct, complete formal proof that can be verified in Lean 4.
    """
    
    response = client.chat.completions.create(
        model="deepseek-prover-v2",
        messages=[
            {"role": "system", "content": system_prompt},
            {"role": "user", "content": problem_description}
        ],
        temperature=0.3,
        max_tokens=4096
    )
    
    solution = response.choices[0].message.content
    return solution

# 主函数
if __name__ == "__main__":
    # 示例1：证明平方根2是无理数
    sqrt2_proof = prove_sqrt2_irrational()
    print("\n平方根2无理数证明:\n" + "="*50)
    print(sqrt2_proof)
    print("="*50)
    
    # 示例2：解决一个更复杂的数学问题（AIME类型问题）
    aime_problem = """
    证明以下AIME问题：
    
    如果 a, b, c 是正实数且 a + b + c = 3，证明 (a·b)^c + (b·c)^a + (c·a)^b ≤ 3
    
    请提供详细的 Lean 4 形式化证明。
    """
    
    aime_solution = solve_math_problem(aime_problem)
    print("\nAIME问题解决方案:\n" + "="*50)
    print(aime_solution)
    print("="*50)

DeepSeek-Prover-V2 API 最佳实践

为了充分利用 DeepSeek-Prover-V2 API 的强大能力，建议遵循以下最佳实践：

  1. 清晰定义问题

    • 提供精确的数学问题描述
    • 明确说明所需证明的定理或结论
    • 指定使用的数学系统和符号（如 Lean 4）

  2. 结构化提示词

    • 将复杂问题分解为可管理的部分
    • 在提示中包含您期望的证明风格
    • 提供关键概念的背景信息

  3. 温度参数调整

    • 对于形式化证明，使用较低的温度值（0.1-0.3）提高准确性
    • 对于创造性证明思路探索，可以适当提高温度（0.4-0.7）

  4. 迭代改进

    • 如果初始证明不完整，逐步提供反馈
    • 使用模型输出作为下一轮提示的一部分
    • 结合人类专家审查，优化生成的证明

  5. 集成开发环境

    • 考虑将 API 集成到 Lean 4 开发环境中
    • 使用自动验证工具检查生成的证明
    • 建立证明库，用于复用常用定理和引理

DeepSeek-Prover-V2 API 常见问题

问题1：DeepSeek-Prover-V2 与其他数学模型相比有什么优势？

DeepSeek-Prover-V2 最显著的优势在于其专为 Lean 4 形式化定理证明设计的特性。与通用数学模型相比，它能够：

  • 生成符合 Lean 4 语法和规范的完整形式化证明
  • 在 MiniF2F 测试集上达到 88.9% 的通过率，远超其他模型
  • 使用递归证明搜索方法处理复杂问题，有效分解和解决子目标
  • 结合非形式化数学推理和形式化证明，提供更全面的数学思维过程

问题2：使用 DeepSeek-Prover-V2 需要具备哪些先验知识？

虽然 DeepSeek-Prover-V2 能够处理复杂的数学证明，但以下先验知识会帮助您更有效地使用它：

  • 基本的数学证明概念和方法
  • Lean 4 语法和使用经验（如果需要验证或修改生成的证明）
  • 形式化方法的基础知识
  • 特定数学领域的专业知识（根据您的应用场景）

对于初学者，建议从简单的定理证明开始，逐步探索模型的能力。

问题3：DeepSeek-Prover-V2 生成的证明如何验证？

生成的形式化证明可以通过以下方式验证：

  • 在 Lean 4 环境中直接运行和检查
  • 使用自动定理证明工具进行验证
  • 结合人工审查，特别是对于复杂证明
  • 与现有已知证明进行对比

API易还提供了验证服务，可以帮助确认生成的证明是否符合 Lean 4 的形式要求并正确无误。

问题4：如何处理特别复杂的证明问题？

对于特别复杂的证明问题，建议：

  • 将问题分解为多个子问题或引理
  • 采用递归证明方法，类似 DeepSeek-Prover-V2 的训练方式
  • 结合 DeepSeek-V3 进行高级策略规划，再使用 DeepSeek-Prover-V2 进行形式化
  • 增加上下文信息，提供相关背景知识和定理
  • 在多次调用之间保持证明状态，实现复杂证明的分步构建

为什么选择 API易 AI大模型聚合平台

  1. 独家提供 DeepSeek-Prover-V2 稳定供给

    • 官方源头转发，确保模型性能与原版一致
    • 稳定的 API 调用体验，无限制使用
    • 当官方平台暂停充值或限流时，API易仍能持续提供服务

  2. 全面的数学模型生态

    • 除 DeepSeek-Prover-V2 外，还提供多种优秀数学模型
    • 一站式访问多种互补能力的模型，满足不同场景需求
    • 模型间无缝切换，享受综合优势

  3. 优化的调用体验

    • 简化的 API 调用流程，与 OpenAI API 兼容
    • 提供详细的使用文档和示例代码
    • 多节点部署，确保低延迟和高可用性

  4. 专业的技术支持

    • 针对数学和定理证明应用场景的专业咨询
    • 7×24 技术支持响应
    • 定制化解决方案开发

  5. 合理的价格策略

    • 透明定价：Input: $0.5 / M Tokens，Output: $2 / M Tokens
    • 新用户优惠：赠送 1.1 美金额度，约 300万 Tokens 体验
    • 无最低消费限制，按量计费

提示：DeepSeek-Prover-V2 是定理证明和形式化方法领域的重要突破，API易平台提供的稳定服务使这一强大能力能够被更广泛地应用于研究、教育和软件开发。无论您是数学研究人员、教育工作者还是形式化方法从业者，都能通过 API易 快速上手并充分利用这一创新模型。

总结

DeepSeek-Prover-V2 代表了形式化定理证明领域的重要进步，其创新的递归证明搜索和基于强化学习的训练方法，使其在复杂数学问题处理方面表现卓越。特别是在 Lean 4 环境中，该模型能够将非形式化数学思维与严格的形式化证明无缝结合，为数学研究、教育和软件验证等领域带来革命性的工具。

通过 API易 平台，您现在可以轻松访问这一强大的模型能力，无需担心供应不稳定或访问限制的问题。无论是处理高难度的数学证明、辅助教学，还是进行软件形式化验证，DeepSeek-Prover-V2 都能提供专业而精确的支持。

随着形式化方法在软件工程和科学研究中的重要性日益提升，掌握和应用 DeepSeek-Prover-V2 这样的前沿工具将为您的工作带来显著优势。现在，就通过 API易 平台开始探索形式化定理证明的新可能性吧！

欢迎免费试用 API易，3 分钟跑通 API 调用 www.apiyi.com
支持 DeepSeek-Prover-V2 等全系列模型，让形式化定理证明更简单
加站长个人微信：8765058，发送你《大模型使用指南》等资料包，并加赠 1 美金额度。

CTA：免费试用 API易

本文作者：API易团队

欢迎关注我们的更新，持续分享 AI 开发经验和最新动态。

免费试用 API易 https://www.apiyi.com
稳定可靠的大模型API聚合服务， 新用户注册就送300万Tokens

类似文章